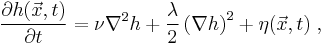Kardar–Parisi–Zhang equation

The KPZ-equation (named after its creators Mehran Kardar, Giorgio Parisi, and Vi-Cheng Zhang) is a non-linear stochastic partial differential equation. It describes the temporal change of the height 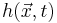$h(\vec x,t)$ at place 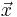$\vec x$ and time $t$ . It is given by

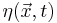$\frac{\partial h(\vec x,t)}{\partial t} = \nu \nabla^2 h %2B \frac{\lambda}{2} \left(\nabla h\right)^2 %2B \eta(\vec x,t) \; ,$

where $\eta(\vec x,t)$ is white Gaussian noise with average 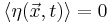$\langle \eta(\vec x,t) \rangle = 0$ and second moment 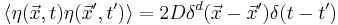$\langle \eta(\vec x,t) \eta(\vec x',t') \rangle = 2D\delta^d(\vec x-\vec x')\delta(t-t')$ . $\nu$ , $\lambda$ , and $D$ are parameters of the model and $d$ is the dimension.

By use of renormalization group techniques it can be shown that the KPZ-equation is the field theory of many surface growth models, such as the Eden model, ballistic deposition, and the SOS model.

Sources

Mehran Kardar, Giorgio Parisi, and Yi-Cheng Zhang, Dynamic Scaling of Growing Interfaces, Physical Review Letters, Vol. 56, 889 - 892 (1986). APS
A.-L.Barabási and H.E.Stanley, Fractal concepts in surface growth (Cambridge University Press, 1995)